Bangun Ruang
Hai, reader yang budiman! welcome to my blog Pembelajaran Matematika. Today, kita akan membahas materi yang spesial nih, yaitu bangun ruang. well, sebelumnya materi ini sudah pernah kita temui saat masih Sekolah Dasar ya! Jadi, pada postingan kali ini kita akan mengulang kembali materi Bangun Ruang edisi Sekolah Dasar.
Masih ingat gak ya......... ?
Nah, untuk pemanasannya nih, coba reader lihat gambar berikut ini.
Nah, dalam kehidupan sehari-hari, kita sering berjumpa dengan benda-benda pada gambar di atas ya! yang suka main rubik, main bola, main telepon kaleng, dan lain-lain. Tanpa sadar masa kecil kita ternyata sudah dekat nih dengan bangun ruang.
Kenapa di sebut bangun ruang ?
beberapa benda disebut bangun ruang karena dia berbentuk tiga dimensi dengan ruang yang dibatasi sisi-sisinya. Bisa dikatakan yang membedakan bangun ruang dengan bangun datar adalah adanya volume.
A. Pengertian Bangun Ruang
Bangun ruang adalah sebuah penamaan atau sebutan untuk beberapa bangun-bangun yang berbentuk tiga dimensi atau bangun yang mempunyai ruang yang dibatasi oleh sisi-sisinya.
Umumnya ada 7 macam bangun ruang yang kita pelajari. Yuk simak pembahasannya!
B. Macam-Macam Bangun Ruang
1. Kubus
"Kubus ialah sebuah bangun ruang yang memiliki panjang rusuk yang sama serta merupakan bangun yang di batasi oleh enam buah sisi yang sama dan sebangun, serta merupakan bangun ruang tiga dimensi."
Sifat-Sifat Kubus:
- Mempunyai 6 sisi berbentuk persegi yang ukurannya sama luas
- Mempunyai 12 rusuk yang ukurannya sama panjang
- Mempunyai 8 titik sudut
- Mempunyai 4 buah diagonal ruang
- Mempunyai 12 buah bidang diagonal
Rumus Kubus:
- Luas salah satu sisi kubus, rumusnya: s2
- Luas permukaan kubus, rumusnya: 6xs2
- Rumus volume, rumusnya: S3
- Rumus keliling, rumusnya: 12xs
Keterangannya:
L= Luas permukaan kubus (cm2)
V= Volume kubus (cm3)
S= Panjang rusuk kubus (cm)
2. Balok
"Balok ialah bangun ruang tiga dimensi yang dibentuk dari tiga pasang persegi atau persegi panjang, dengan setidaknya memiliki satu pasang di antaranya berukuran berbeda."
Sifat-Sifat Balok :
- Mempunyai 4 sisi berbentuk persegi panjang (2 pasang persegi panjang yang ukurannya sama)
- Mempunyai 2 sisi yang bentuknya sama (1 pasang persegi panjang dengan ukurannya sama namun berbeda ukuran dengan 2 pasang persegi panjang yang lain)
- Mempunyai 12 rusuk yang ukurannya sama panjang
- Mempunyai 8 buah titik sudut
Rumus Balok:
1. Rumus untuk permukaan balok= 2x(pxl)+(pxt)+(lxt)
2. Rumus untuk diagonal ruang= Akar dari(p kuadrat+l kuadrat+t kuadrat)
3. Rumus untuk keliling balok= 4x(p+l+t)
4. Rumus untuk volume balok= pxlxt
Keterangannya :
P adalah Panjang (cm)
L adalah Lebar (cm)
T adalah Tinggi (cm)
3. Limas
"Limas adalah sebuah bangun ruang 3 dimensi yang memiliki alas yang berbentuk segi banyak dan bidang tegaknya berbentuk segitiga dan salah satu sudutnya bertemu di satu titik."
Sifat-Sifat Limas:
- Mempunyai 5 sisi yaitu: 1 sisi berbentuk segiempat yang merupakan alas dan 4 sisi lainnya semuanya berbentuk segitiga serta merupakan sisi tegak.
- Mempunyai 8 buah rusuk
- Mempunyai 5 titik sudut yaitu: 4 sudut berada di bagian alas dan 1 sudut berada di bagian atas yang merupakan titik puncak.
Rumus Limas:
1. Rumus untuk Mencari Volume = 1/3 x luas alas x tinggi sisi
2. Rumus untuk Mecari Luas = luas alas+jumlah luas sisi tegak
4. Bola
"Bola adalah
sebuah bangun ruang sisi lengkung yang dibatasi oleh satu bidang lengkung."
Sifat-sifat Bola:
- Mempunyai alas berbentuk segienam
- Mempunyai 6 sisi
- Mempunyai 10 rusuk
- Mempunyai 6 titik sudut
Rumus-Rumus Bola :
Rumus untuk mencari volume bola yaitu: 4/3 x π x r3
Rumus untu mencari luas bola yaitu : 4 x π x r2
Keterangan:
V : Volume bola (cm3)
L : Luas permukaan bola (cm2)
R : Jari – jari bola (cm)
Ï€ : 22/7 atau 3,14
5. Kerucut
"Kerucut adalah salah satu bangun ruang yang mempunyai sebuah alas yang berbentuk lingkaran dengan selimut yang memiliki irisan dari lingkaran."
Sifat-Sifat Kerucut:
- Mempunyai 2 sisi (1 sisi merupakan alas yang berbentuk lingkaran dan 1 sisinya lagi berupa sisi lengkung atau selimut kerucut)
- Mempunyai 1 rusuk
- Mempunyai 1 titik sudu
Rumus Kerucut:
Rumus untuk mencari volume = 1/3 x π x r x r x t
Rumus untuk mencari luas = luas alas+luas selimut
Keterangan:
- r = jari – jari (cm)
- T = tinggi(cm)
- π = 22/7 atau 3,14
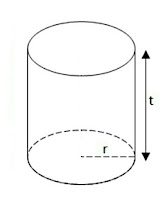
6. Tabung
"Bangun Tabung adalah sebuah bangun ruang tiga dimensi yang memiliki tutup dan alas yang berbentuk lsebuah ingkaran dengan ukuran yang sama dengan di selimuti oleh persegi panjang."
Sifat-Sifat Tabung:
- Mempunyai 3 sisi ( 2 sisi berbentuk lingkaran dan 1 sisi berupa selimut tabung )
- Mempunyai 2 rusuk
Rumus – Rumus pada Tabung
- Rumus luas alas= luas lingkaran=Ï€ x r2
- Rumus volume pada tabung= π x r2 x t
- Rumus keliling alas pada tabung= 2 x π x r
- Rumus luas pada selimut tabung = 2 x π x r x t
- Rumus luas pada permukaan tabung= 2 x luas alas+luas selimut tabung
- Rumus kerucut + tabung =
- volume = ( π.r2.t )+( 1/3.π.r2.t )
- luas = (Ï€.r2)+(2.Ï€.r.t)+(Ï€.r.s)
- Rumus tabung + 1/2 bola =
- Rumus Volume = π.r2.t+2/3. π.r3
- Rumus Luas = (Ï€.r2)+(2.Ï€.r.t)+(½.4.n.r2) = (3.Ï€.r2)+(2. Ï€ .r.t)
- Rumus tabung+bola
- Volume= (π.r2.t)+(4/3. π.r3)
- Luas= (2. π.r2)+(4. π.r2) = π.r2
Keterangannya:
- V = Volume tabung(cm3)
- π = 22/7 atau 3,14
- r = Jari – jari /setengah diameter (cm)
- t = Tinggi (cm)
7. Prisma
"Prisma dapat didenisikan sebuah hasil dari gabungan antara bangun datar 2 dimensi baik dari bangun datar persegi panjang atau bangun datar segitiga."
Sifat-Sifat Prisma:
- Mempunyai bidang alas dan bidang atas berupa segitiga yang kongruen (2 alas tersebut juga merupakan sisi prisma segitiga)
- Mempunyai 5 sisi (2 sisi berupa alas atas dan bawah, 3 sisi lainnya merupakan sisi tegak yang semuanya berbentuk segitiga)
- Mempunyai 9 rusuk
- Mempunyai 6 titik sudut
Rumus Prisma:
- Untuk mencari luas: Luas = (2 x luas alas) + (luas seluruh bidang tegak)
- Untuk mencari keliling : K = 3s (s + s + s)
- Untuk mencari Volume :
Volume Prisma = Luas segitiga x tinggi
Volume Prisma = 1/2 x a.s x t.s x t
Nah, sekian pembahasan kali ini dan jangan lupa budayakan like, share, dan komen jika bermanfaat bagi anda dan bermanfaat bagi kita semua.
Selamat Membaca
Tidak ada komentar